Contrary to common misunderstanding, the credibility assigned to a mortality study has nothing to do with quality of underwriting that went into its underlying business. Certainly the overall mortality rate is correlated with the distribution of risk factors including underwriting class, age, gender, and even product type. However, it is the number of deaths in the experience study that determines the level of confidence placed in the overall study results.
Example Redux
To demonstrate the connection between confidence level and claim count, let’s take another look at the example from Part 1 of this series. As you recall, we had 20,000 risks each having a mortality rate of 0.00125. Our 10,000 random trials produced an average of 25 deaths. Now let’s triple our mortality rate in order to simulate a substandard risk class. Charts 1 and 2 show the results from the original example and our newly defined substandard group.
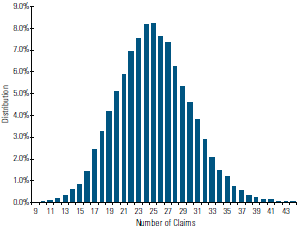
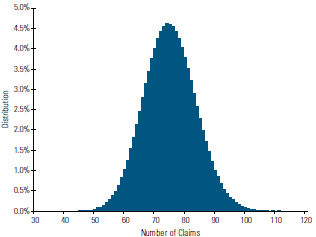
All else being equal, the higher mortality rate has produced triple the average number of claims. More importantly, the range of outcomes as a percentage of the mean has decreased.
For the original mortality rate, only 73 percent of the claim counts fall between plus or minus 20 percent of the mean. With triple the mortality, nearly 93 percent of the counts are between plus or minus 20 percent of the mean. Thus, a higher mortality rate results in higher average claim counts and increased confidence in predicting the outcome of any one trial as a percentage of the mean.
Defining Full Credibility
An experience study is the result of one random sample from a population being exposed to a process of mortality. The mortality rate from that one sample is assumed to be the best representation (our “best guess”) of the true mortality arising from the population. Credibility provides a quantitative measure of how good our guess is.
How can we make the determination that a study’s overall results are credible enough to use as the basis for a pricing assumption? There is no single correct answer to when a study’s results are deemed “fully credible.” An actuary can objectively state that future mortality is likely to be within plus or minus X percent of a current experience study’s results Y percent of the time, but someone needs to determine the X and Y percentages. In my mind, the values chosen for these critical parameters are business decisions rather than statistical decisions.
One company may decide that they will rely upon a current study as representative of future experience when the statement can be made that future mortality will be within five percent (“X”) of the current study mortality 95 percent (“Y”) of the time. Another company may require future mortality expectations to be within one percent of the study experience 99 percent of the time before using the study results as a pricing assumption.
Practical Aspects
A key consideration in choosing parameter values is the probability that the study result is not a good representation of the true population mortality. Due to random fluctuations, our study just happened to produce mortality results that are significantly different than the population trend. Analyzing this probability gets into the realm of what statisticians call hypothesis testing, which is beyond the scope of this series of articles. Suffice it to say that the lower the claim count, the higher the likelihood that our study is not an accurate prediction of future mortality.
Another practical aspect in the company’s parameter decision is the number of claims required for full credibility. Chart 3 shows the range of claims for various combinations of parameter values.
Chart 3 - Number of Claims Needed for Full Credibility
|
Prob |
10.0% 7.5% |
5.0% 4.0% |
3.0% |
2.0% |
1.0% |
|
80% |
164 |
|
|
292 |
|
657 |
1,027 |
1,826 |
4,109 |
16,435 |
|
85% |
207 |
|
|
369 |
|
829 |
1,296 |
2,304 |
5,184 |
20,736 |
|
90% |
271 |
|
|
481 |
|
1,082 |
1,691 |
3,007 |
6,765 |
27,060 |
|
95% |
384 |
|
|
683 |
|
1,537 |
2,401 |
4,268 |
9,604 |
38,416 |
Choosing the critical parameters (probability of accuracy with a given percentage
range) of a study is a business decision. If full credibility is required, that decision must take into account the amount of claims data that the company has available.
For example, if we wanted to be able to predict that future mortality would be within plus or minus one percent of the study results 95 percent of the time, we would want the study to have at least 38,416 claims. A company that chooses too stringent a rule may never a have a study that earns full credibility status.
Partial Credibility
What happens when an experience study is deemed to be less than fully credible?
The final installment in this series will show how credibility theory can be used to weight study results with other experience to determine a more appropriate mortality assumption.